Page 369 - Science and Technology For Society 5.0

332 ~ Seminar Internasional FST UT 2021 ~

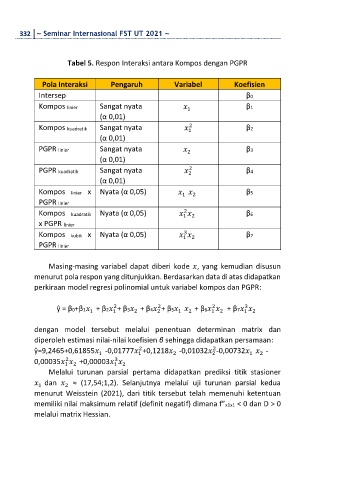
Tabel 5. Respon Interaksi antara Kompos dengan PGPR

Pola Interaksi Pengaruh Variabel Koefisien
Intersep β0
Kompos linier Sangat nyata β1
1
(α 0,01)
2
Kompos kuadratik Sangat nyata β2
1
(α 0,01)
PGPR linier Sangat nyata β3
2
(α 0,01)
2
PGPR kuadratik Sangat nyata β4
2
(α 0,01)
Kompos linier x Nyata (α 0,05) β5
1
2
PGPR linier
2
Kompos kuadratik Nyata (α 0,05) β6
1 2
x PGPR linier
3
Kompos kubik x Nyata (α 0,05) β7
1 2
PGPR linier

Masing-masing variabel dapat diberi kode , yang kemudian disusun
menurut pola respon yang ditunjukkan. Berdasarkan data di atas didapatkan
perkiraan model regresi polinomial untuk variabel kompos dan PGPR:

3
2
2
2
ŷ = β0+β1 + β2 + β3 + β4 + β5 + β6 1 2
1 2 + β7
2
1
2
2
1
1

dengan model tersebut melalui penentuan determinan matrix dan
diperoleh estimasi nilai-nilai koefisien β sehingga didapatkan persamaan:
2
2
ŷ=9,2465+0,61855 -0,01777 +0,1218 -0,01032 -0,00732 -
2
1
2
1
1
2
2
3
0,00035 +0,00003
1 2
1 2
Melalui turunan parsial pertama didapatkan prediksi titik stasioner
dan ≈ (17,54;1,2). Selanjutnya melalui uji turunan parsial kedua
2
1
menurut Weisstein (2021), dari titik tersebut telah memenuhi ketentuan
memiliki nilai maksimum relatif (definit negatif) dimana f”x1x1 < 0 dan D > 0
melalui matrix Hessian.